-
ابزار گرافیکی در EDA
- تاکید در EDA تعامل بین شناخت انسان و محاسبات به صورت گرافیک آماری است که اجازه می دهد کاربر رفتار و ساختار داده را درک کند.
- در میان انواع مختلفی از ابزارهای گرافیکی EDA،(Tukey, 1977; Velleman And Hoaglin, 1981; Chambers et al., 1983)، شاخص چگالی، نمودار پراکندگی تک بعدی و نمودار جعبه ای معمولا در تجزیه و تحلیل داده های ژئوشیمیایی تک عنصری استفاده می شوند (Howarth and Turner, 1987; Kürzl, 1988; Reimann et al., 2005; Grunsky, 2006). این سه نمودار EDA ، که به آسانی می توانند روی یکدیگر قرار بگیرند (شکل1)، اغلب با هم به همراه یک هیستوگرام استفاده می شوند. علت آن است که برداشت بصری از رفتار و ساختار داده تک متغییره که از یک هیستوگرام بدست می آید تنها متاثر از انتخاب تعداد کلاس های لازم برای بدست آوردن هیستوگرام هاست. ترکیبی از سه نمودار EDA با هیستوگرام دید بهتری از رفتار و ساختار داده تک متغییره نسبت به هیستوگرام تنها فراهم می کند. برخلاف یک هیستوگرام، سه نمودار EDA به آسانی می توانند هر اختلال در مجموعه داده تک متغییره را نشان دهند.
-
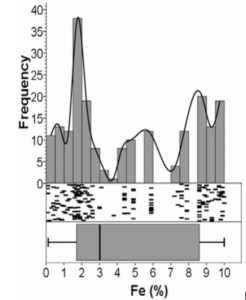
شکل 1- هیستوگرام و نمودارهای EDA(شاخص چگالی، نمودار پراکندگی تک بعدی، نمودار جعبه ای)
- شاخص چگالی شبیه یک هیستوگرام است اما آن توزیع چگالی تجربی داده های تک متغییره را به شیوه ای بسیار واقعی تر توصیف می کند و با تغییر در تعداد کلاس ها تغییر قابل توجهی در شکل آن ایجاد نمی کند. تعداد مناسب از کلاس ها برای ساخت یک هیستوگرام را می توان با ساخت یک نمودار پراکندگی تک بعدی کنترل کرد که در آن داده های تک متغییره در موقعیت های تصادفی در یک باند باریک (معمولا با طیف وسیعی از 1-0) عمود بر محور داده ی تک متغییره رسم می شود. به دلیل آنکه نمودار پراکندگی تک بعدی براساس کلاس های داده های تک متغییره نیست، آن اطلاعات اضافی در مورد داده ها فراهم می کند (ساختار، رفتار، تراکم محلی، شکاف، نقاط خارج از ردیف) که باید توسط یک هیستوگرام و شاخص چگالی به تصویر کشیده شود. نمودار جعبه ای(box plot) اطلاعاتی درباره ویژگی های توزیع چگالی تجربی(تمایل مرکزی، گسترش و …) از مجموعه داده های تک متغییره را نمایش می دهد. همچنین احتمالا مفیدترین ابزار گرافیکی EDA در تجزیه و تحلیل داده های اکتشافی است و بنابراین اینجا توجه خاصی به آن شده است.–
-
نمودار جعبه ای و 5 آمار داده ی تک متغییره
- نمودار جعبه ای توسط اولین مقادیر داده ها از کوچک ترین تا بزرگ ترین یا بالعکس آن ایجاد می شود (شکل2). سپس مقدار میانه با شمارش نیمی از مقادیر داده ها از مینیمم تا ماکسیمم یا بالعکس تعیین می شود که نتیجه آن تقسیم مجموعه داده های تک متغییره به دو بخش مساوی است. به وسیله ی روش شمارش نیمی از داده ها از مینیمم تا میانه و از ماکسیمم تا میانه، به ترتیب مقدار محور پایین(LH) و محور بالا (UH) تعیین می شود. محور پایین، متوسط و محور بالا، در نتیجه مجموعه دادها به چهار بخش تقریبا مساوی به عنوان چارک تقسیم می شوند. مقادیر مینیمم تا محور پایین تر نشان دهنده ی چارک اول (Q1) از مجموعه داده هاست، از مقادیر محور پایین تر تا میانه نشان دهنده ی چارک دوم (Q2) است، از مقدار میانه تا محور بالا نشان دهنده ی چارک سوم(Q3) است و از مقادیر محور بالا تا ماکسیمم نشان دهنده ی چارک چهارم(Q4) می باشد. سپس یک جعبه بین محورهای پایین و بالا رسم می شود. پس از آن جعبه معمولا توسط یک خط در مقدار میانه تقسیم می شود. تفاوت مطلق بین مقادیر پایین و بالای محور نشان دهنده ی محدوده ی بین چارک(IQR) و یا عرض محور است.
-
عرض محور = IQR= |محورپایین – محور بالا|
-
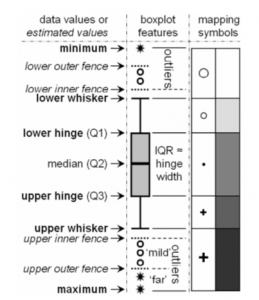
شکل2- ویژگی های نمودار جعبه ای نشان دهنده ی ویژگی های یک مجموعه داده های تک متغییره، متن ایتالیک نشان دهنده ی مقادیر تخمین زده شده براساس محدوده ی بین چارک(IQR) و عرض محور است. متن ضخیم نشان دهنده ی مقادیر داده است که در آن می توان یک مجموعه داده تک متغییره را به پنج کلاس تقسیم کرد. هر کلاس به وسیله نمادهای رسم نقشه –EDA یا رنگهای خاکستری در اینجا نشان داده می شود.
- حد پایینی تر داخلی (LIF) و حد پایین تر خارجی(LOF) به ترتیب به صورت 1.5*IQR و 3*IQRتعریف می شوند که از محور پایین به سمت مقدار مینیمم هستند. از لحاظ جبری مقادیر (X) در (LIF) و (LOF)می توانند به ترتیب به….